
Let there be four vertices v1, v2, v3 and v4 in the network whose normalized BWC values are 0.49, 0.62, 0.11, and 0.79, respectively, and normalized CLC values are 0.38, 0.42, 0.87, and 0.48, respectively. For example, let BWC and CLC be the two node-level metrics considered. We propose that two vertices are to be considered “similar” with respect to a set of node-level metrics if the vertices are “closer” on the basis of the Euclidean distance between their coordinates (represented by the normalized values of the node-level metrics for the vertices in the network). In this paper, we seek to develop a “network-level” node similarity index (NSI) to comprehensively quantify the extent of similarity (in a scale of 0 to 1) among “all” the nodes in a network with respect to a set of node-level metrics. There is currently no quantitative measure available to rate the extent of similarity among all the vertices in a network with respect to a combination of node-level metrics (topological metrics and/or domain-based metrics). Also, the currently available similarity measures (like assortative index ) use just one node-level metric (typically, the degree centrality metric) to assess the similarity between two vertices or a set of vertices.
It would not be appropriate to quantify the similarity among all the nodes in a network as a statistical function (like average or median) of the pair-wise similarity metric values. To the best of our knowledge, all the similarity measures available in the literature quantify the extent of similarity between two nodes (like cosine similarity, matching index, etc.) or a set of nodes (the notion of equivalence classes, Rich club coefficient, etc.), but not among all the nodes in a network. Similarity assessment of nodes in complex networks has been so far conducted only at the node-level (e.g., ) and not at the network-level. Throughout the paper, the terms 'node' and 'vertex', 'link' and 'edge', and 'network' and 'graph' are used interchangeably. Some of the examples for domain-based metrics are age, height, and weight of a patient (health information networks), number of publications and h-index of an author (citation networks), the processing capacity and the number of ports available for a router (communication networks), etc. More detailed information about these four centrality metrics and the procedures to individually compute them is available in. While DEG and EVC could be categorized as neighborhood-based centrality metrics, BWC and CLC could be categorized as shortest path-based centrality metrics. There exist several centrality metrics, each proposed to capture a particular topological aspect the four commonly studied centrality metrics are degree centrality (DEG), eigenvector centrality (EVC), betweenness centrality (BWC), and closeness centrality (CLC). Centrality metrics quantify the topological importance of the nodes in a network. vertices) in a complex network are either topology-based or domain-based or a combination of both. We evaluate the NSI values for a suite of 60 real-world networks with respect to both neighborhood-based centrality metrics (degree centrality and eigenvector centrality) and shortest path-based centrality metrics (betweenness centrality and closeness centrality). We refer to “1 − (minimum threshold distance )” as the node similarity index (NSI ranging from 0 to 1) for the complex network with respect to the k node-level metrics considered.
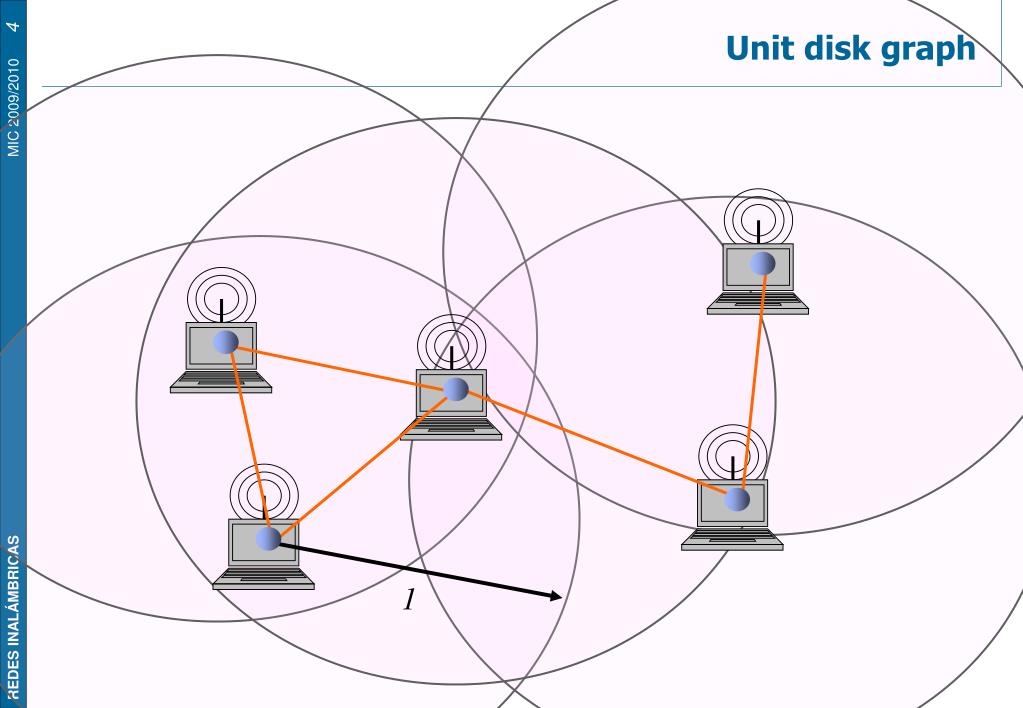
We run a binary search algorithm to determine the minimum value for the threshold distance that would yield a connected unit disk graph of the vertices. There exists an edge between two vertices in the unit disk graph if the Euclidean distance between the two vertices in the normalized coordinate system is within a threshold value (ranging from 0 to, where k is the number of node-level metrics considered). In this pursuit, we propose the following unit disk graph-based approach: we first normalize the values for the node-level metrics (using the sum of the squares approach) and construct a unit disk graph of the network in a coordinate system based on the normalized values of the node-level metrics. We seek to quantify the extent of similarity among nodes in a complex network with respect to two or more node-level metrics (like centrality metrics).


 0 kommentar(er)
0 kommentar(er)
